Pengonversi Sudut

Sudut ada di mana-mana. Mereka menentukan sudut rumah Anda, kemiringan Bumi, bahkan cara adegan film favorit diambil. Meskipun alat Pengonversi Sudut membuat perpindahan antara derajat, radian, dan revolusi menjadi mudah, konsep sudut memiliki sejarah, kegunaan, dan makna universal yang kaya. Mulai dari astronom Babilonia kuno yang memetakan bintang hingga insinyur modern yang merancang jembatan, sudut membantu kita memahami ruang dan gerak. Mereka mendasari matematika, fisika, seni, bahkan filsafat. Dalam artikel ini, kita tidak hanya akan menjelaskan cara mengonversi sudut—kita juga akan mengeksplorasi mengapa sudut penting dalam ilmu pengetahuan, budaya, dan kehidupan sehari-hari. Baik Anda pelajar, peneliti, maupun pembaca yang penasaran, perjalanan ini akan mengungkap bagaimana hal sesederhana putaran atau sudut dapat membuka geometri tersembunyi alam semesta.

Apa Itu Sudut?

Sudut bukan sekadar sudut tajam pada diagram—itu adalah konsep fundamental dalam cara kita memahami dan menggambarkan dunia di sekitar. Menurut National Institute of Standards and Technology (NIST), sudut didefinisikan sebagai “bentuk yang dibentuk oleh dua sinar yang memiliki titik awal sama,” dan diukur dari besarnya rotasi satu sinar hingga sejajar dengan sinar lainnya.

Dalam praktiknya, sudut ada di mana-mana—dari cara kita memiringkan kepala hingga bagaimana kita membangun jembatan dan memutar satelit. Mereka membantu kita menafsirkan arah, orientasi, bahkan keseimbangan. Tanpa sudut, geometri akan runtuh, rekayasa jadi tebakan, dan gerak pun kehilangan makna matematis.

Sudut hadir dalam berbagai bentuk:

Setiap jenis memiliki signifikansi di dunia nyata. Sudut lancip dan siku mendominasi struktur sehari-hari—dinding, layar, dan tepi kertas—sementara sudut tumpul dan refleks muncul dalam desain, arsitektur, dan biomekanika. Dalam fisika, gerak sudut menjelaskan segalanya mulai dari orbit planet hingga putaran elektron. Bahkan dalam persepsi, sudut berperan: persepsi kedalaman kita bergantung pada sudut pandang visual yang dibentuk oleh mata.

Derajat, Radian, dan Revolusi

Sudut mungkin tampak sederhana, tetapi cara pengukurannya berevolusi melalui sejarah, matematika, hingga budaya. Tiga satuan paling umum—derajat, radian, dan revolusi—membentuk sistem universal yang memungkinkan kita mendeskripsikan rotasi, orientasi, dan gerak di berbagai disiplin.

Hubungan Inti

Rotasi penuh pada lingkaran bisa dinyatakan setara dalam tiga satuan:

Dari sini, kita dapat merumuskan konversi utama:

Kesetaraan ini tidak hanya untuk matematikawan—mereka menjadi dasar animasi digital hingga perhitungan orbit dalam penerbangan antariksa.

Apa Itu Radian?

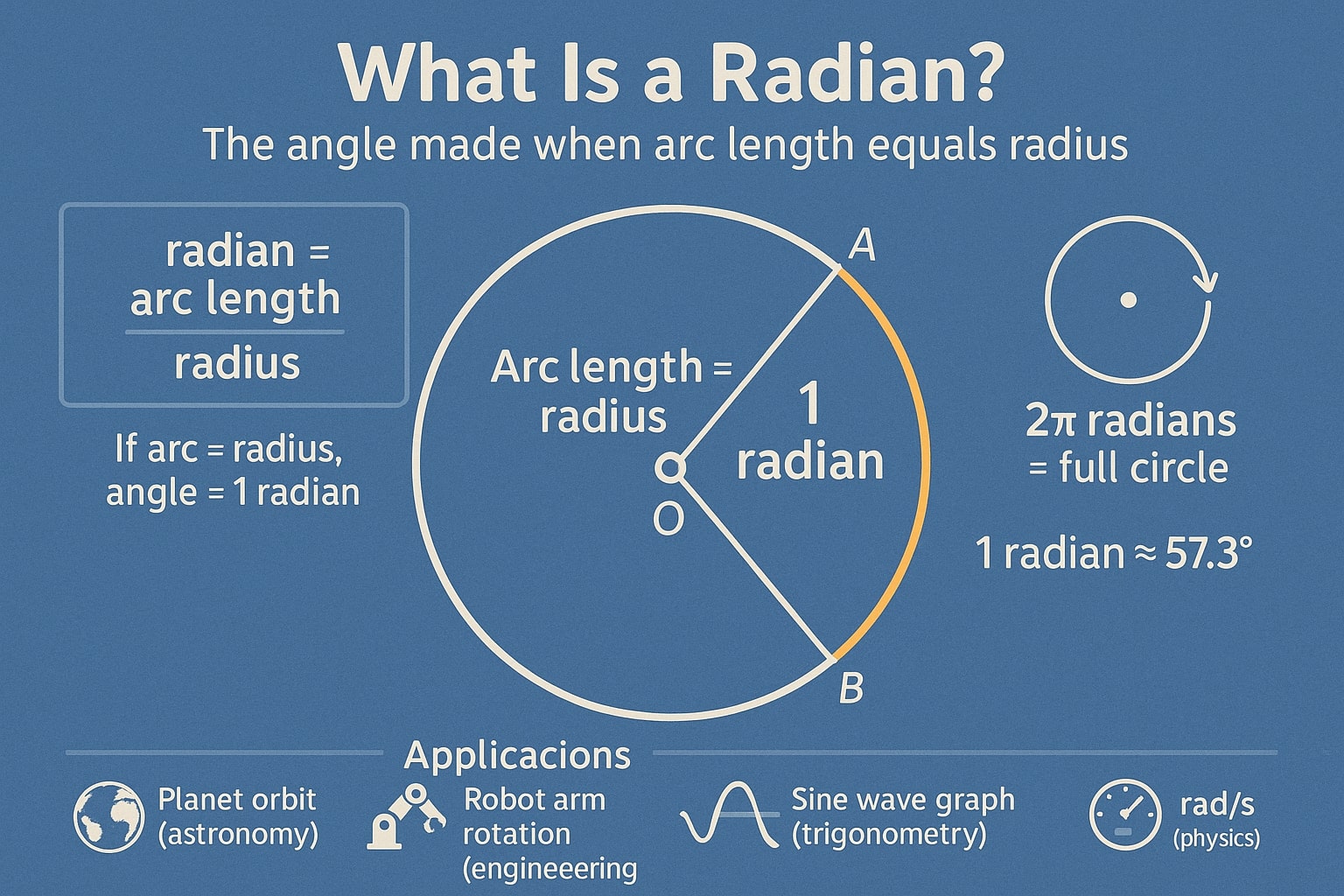
Radian adalah satuan pengukuran sudut standar dalam matematika lanjut dan fisika, yang didasarkan pada jari-jari lingkaran. Satu radian didefinisikan sebagai sudut yang dibentuk ketika panjang busur sama dengan jari-jari lingkaran.
Secara matematis:

radian = panjang busur / jari-jari

Karena keliling lingkaran adalah 2πr, satu putaran penuh setara dengan 2π radian.
Dengan demikian:

Radian mempermudah banyak persamaan matematika, terutama dalam kalkulus, di mana fungsi trigonometri berperilaku lebih alami dan ringkas saat diukur dalam radian.

Rumus Konversi Inti

Formula-formula ini memudahkan konversi antar sistem, baik saat Anda memrogram, memplot grafik, maupun menafsirkan data ilmiah.

Tabel Cepat untuk Sudut Umum

Tabel ini sangat berguna bagi pelajar dan profesional yang bekerja dengan fungsi trigonometri, gerak melingkar, atau lingkungan pemrograman seperti JavaScript dan Python.

Kesalahan Umum dalam Konversi Sudut

• Lupa mengganti mode kalkulator: Banyak orang menggunakan derajat saat seharusnya radian (atau sebaliknya), sehingga menghasilkan nilai trigonometri yang keliru.

• Salah mengelola π: Membulatkan π terlalu awal dapat menyebabkan hilangnya presisi—terutama di bidang fisika atau teknik.

• Mencampur simbol dan asumsi: Beberapa perangkat lunak ilmiah menganggap sudut dalam radian kecuali dinyatakan lain. Selalu periksa satuan yang diharapkan.

Hubungan Sudut–Waktu dalam Sistem Dunia Nyata

Di dunia yang semakin mengandalkan ketepatan—dari desain digital hingga navigasi antariksa—sudut menjadi bagian krusial dalam cara kita mengukur, memodelkan, dan bergerak melalui waktu. Setiap putaran, setiap lintasan, setiap penyelarasan struktural bergantung pada pengukuran sudut yang tepat—seringkali secara real-time.

Baik Anda siswa yang menghitung radian atau insinyur yang mengatur orientasi satelit, alat Pengonversi Sudut memegang peranan penting. Ia tak hanya menghemat waktu—ia menghargai waktu, memastikan perpindahan mulus antara derajat, radian, dan revolusi tanpa ruang untuk kesalahan.

Jam Analog

• 1 putaran penuh = 360°

• 1 jam = 60°

• 1 menit = 6°
   → Sudut per menit=360/60= 6°

Kecepatan Sudut dalam Robotika / Fisika

• Unit standar pengukuran kecepatan rotasi: radian/detik (rad/s)

• Jika suatu objek berputar θ radian dalam t detik:
   →

di mana ω adalah kecepatan sudut

Revolusi dan Rotasi Berbasis Waktu

• 1 revolusi = 360° = 2π radian

• Waktu per rotasi:
   → Waktu per rev = 1 / Revolusi per detik

Euclid – Bapak Sudut

Jauh sebelum kalkulator atau alat konversi sudut ada, seorang pria membantu membentuk cara kita memahami ruang: Euclid dari Alexandria, sering disebut “Bapak Geometri.” Hidup sekitar 300 SM, karya monumentalnya Elements meletakkan dasar geometri modern—dan dengan itu, konsep sudut kita.

Dalam Elements, Euclid tidak hanya mendefinisikan sudut; ia mensistematisasikannya. Ia menjelaskan sudut siku sebagai hasil ketika sebuah garis tegak berdiri pada garis lain sehingga sudut di sekitarnya sama—sebuah momen keseimbangan dan simetri yang memandu arsitek dan ilmuwan selama ribuan tahun.

Pendekatan ketat Euclid membantu membedakan sudut bukan hanya berdasarkan ukuran, tetapi juga hubungan. Prinsipnya terus memengaruhi arsitektur, astronomi, hingga grafis komputer. Tanpa Euclid, sudut 90° mungkin tak pernah disebut “siku”—bukan hanya dalam nilai, tapi juga namanya.

Untuk menjelajahi lebih banyak alat serupa, kunjungi kategori Konversi—gerbang Anda menuju perhitungan yang lebih cerdas, cepat, dan akurat di bidang fisika, matematika, dan skenario dunia nyata.