Bilangan campuran — seperti 2 ½ atau 5 ¾ — bukan hanya soal matematika di sekolah. Mereka digunakan dalam resep masakan, penjualan kayu, dan pengukuran jarak dalam olahraga.
Bilangan Campuran vs. Pecahan Tidak Biasa
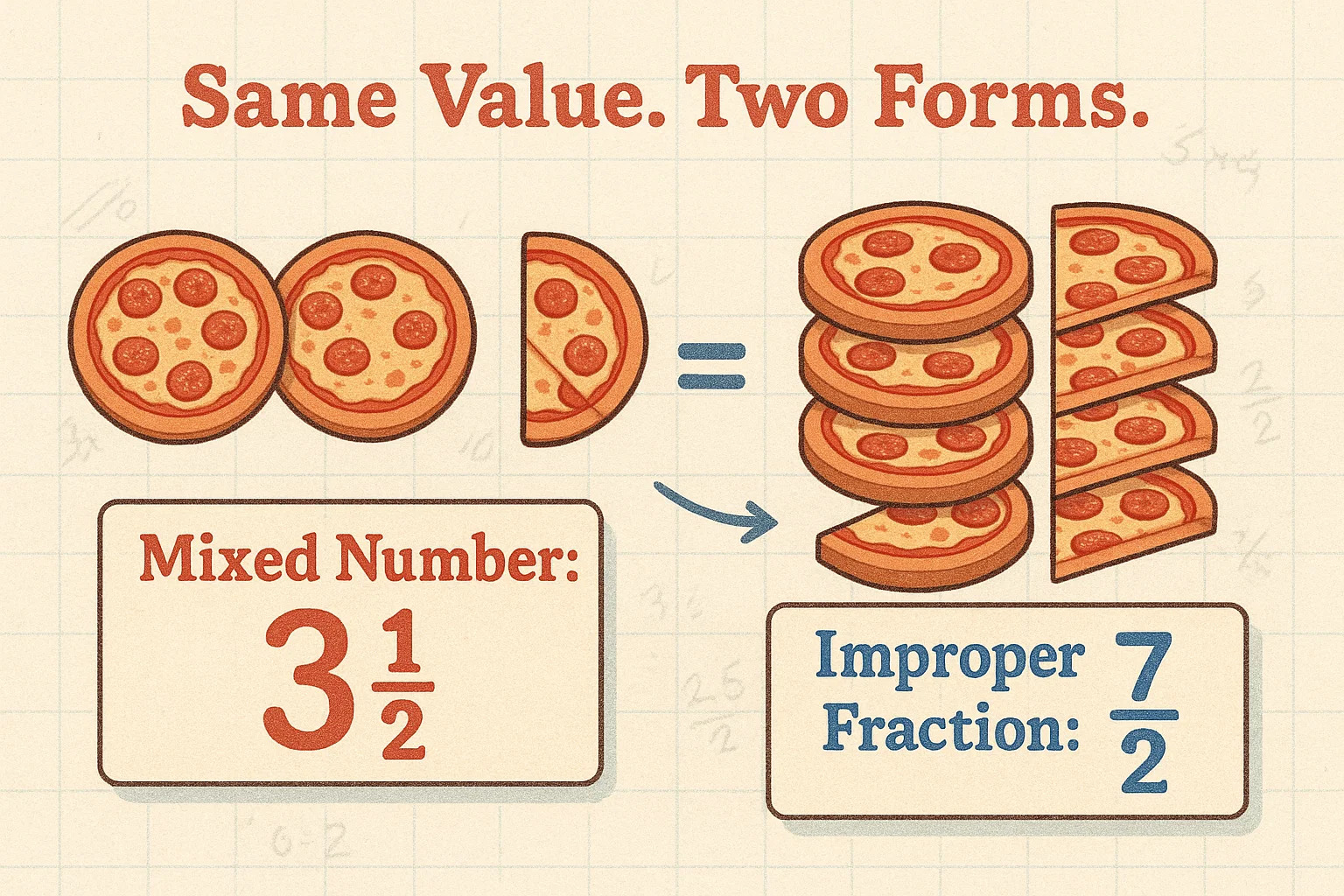
Jika Anda pernah mengukur 2 ½ cangkir tepung atau mendengar seseorang mengatakan mereka berlari sejauh 5 ¾ mil, berarti Anda sudah menggunakan bilangan campuran. Bilangan campuran adalah gabungan angka bulat dan pecahan biasa — misalnya 3 ½, yang artinya tiga utuh ditambah separuh lagi. Mereka praktis, familiar, dan sangat sering digunakan dalam kehidupan sehari-hari.
Sementara itu, pecahan tidak biasa (improper fractions) tampak sedikit rumit tapi mengikuti aturan matematika yang sama. Ini adalah pecahan dengan pembilang (angka atas) sama dengan atau lebih besar dari penyebut (angka bawah) — contohnya ⁷⁄₂. Nilainya sama dengan 3 ½, hanya ditulis berbeda.
Kenapa ada dua cara menulis yang sama? Bilangan campuran lebih mudah dipahami secara langsung, sedangkan pecahan tidak biasa lebih praktis untuk perhitungan, terutama dalam aljabar atau logika pemrograman.
Cara mengubah bilangan campuran menjadi pecahan tidak biasa:
Misalnya 4 ⅗.
- Kalikan angka bulat dengan penyebut: 4 × 5 = 20
- Tambah pembilang: 20 + 3 = 23
- Tulis di atas penyebut asli: ²³⁄₅
Jadi 4 ⅗ menjadi ²³⁄₅.
Ini langkah umum sebelum mengalikan atau membagi bilangan campuran.
Cara mengubah pecahan tidak biasa menjadi bilangan campuran:
Ambil ¹¹⁄₄.
- Bagi pembilang dengan penyebut: 11 ÷ 4 = 2 sisaan 3
- Hasil bagi jadi angka bulat (2), sisaan jadi pembilang baru (3)
- Pertahankan penyebut asli: 2 ¾
Ini cara menyederhanakan bilangan campuran dari format pecahan tidak biasa.
Fakta Menarik: “Dalam misi Apollo 13, insinyur NASA menggunakan alat hitung manual dan operasi pecahan seperti 2 ⁵⁄₈ untuk cepat mengarahkan ulang pesawat luar angkasa dan menyelamatkan kru.” — Arsip NASA¹
Cara Perhitungan Bilangan Campuran Pecahan
Untuk menjumlahkan, mengurangi, mengalikan, atau membagi bilangan campuran, ada trik antara angka bulat dan pecahan. Rahasianya? Jaga perhitungan tetap sederhana dan selalu sederhanakan hasil akhirnya. Baik menggandakan resep atau mengerjakan soal ujian, aturan cepat ini membantu Anda lebih cepat dan akurat.
Penjumlahan dan Pengurangan
Mulai dengan memisahkan angka bulat dan pecahan. Bilangan campuran punya keduanya, jadi proses setiap bagian dulu, lalu gabungkan kembali.
Contoh:
Penjumlahan: 2 ½ + 3 ¾
- Jumlahkan angka bulat: 2 + 3 = 5
- Jumlahkan pecahan: ½ + ¾ → Ubah ke penyebut sama → ²⁄₄ + ³⁄₄ = ⁵⁄₄
- Gabungkan: 5 + ⁵⁄₄, tapi ⁵⁄₄ = 1 ¼, jadi jawabannya: 6 ¼
Pengurangan: 5 ⅚ − 2 ⅔
- Angka bulat: 5 - 2 = 3
- Pecahan: ⁵⁄₆ − ²⁄₃ → Ubah ²⁄₃ jadi ⁴⁄₆ → ⁵⁄₆ − ⁴⁄₆ = ¹⁄₆
- Jawaban akhir: 3 ¹⁄₆
Kalau hasil pengurangan pecahan negatif (misalnya ¼ − ¾), Anda harus meminjam dari angka bulat. Jangan lewatkan langkah ini — di sinilah kesalahan sering terjadi. Anda juga bisa memeriksa hasilnya dengan alat penyederhana pecahan.
Perkalian
Perkalian bilangan campuran selalu diawali dengan mengubahnya dulu.
Misal: Kalikan 2 ⅓ × 1 ½
- Ubah keduanya ke pecahan tidak biasa:
2 ⅓ = ⁷⁄₃
1 ½ = ³⁄₂ - Kalikan pembilang dan penyebut:
⁷⁄₃ × ³⁄₂ = ²¹⁄₆ - Sederhanakan:
²¹⁄₆ = 3 ½
Sekarang Anda siap.
Fakta Tambahan: “Studi di sekolah menengah Chicago menemukan siswa yang berlatih mengubah bilangan campuran sebelum mengalikan meningkatkan nilai ujian hingga 27% dibanding yang hanya menebak berdasarkan visual.” — Studi Departemen Pendidikan AS²
Perkalian lebih langsung karena hanya bekerja dengan angka tanpa harus samakan penyebut seperti pada penjumlahan atau pengurangan. Ragu hasilnya? Coba hitung dulu di kertas, lalu periksa lewat Kalkulator Pecahan.
Pembagian
Pembagian sering dipandang sulit, padahal sebenarnya seperti perkalian terbalik.
Contoh: Bagi 3 ¾ ÷ 1 ½
- Ubah ke pecahan tidak biasa:
3 ¾ = ¹⁵⁄₄
1 ½ = ³⁄₂ - Balik pecahan kedua (pembagi):
³⁄₂ menjadi ²⁄₃ - Kalikan:
¹⁵⁄₄ × ²⁄₃ = ³⁰⁄₁₂ - Sederhanakan:
³⁰⁄₁₂ = 2 ½
Selesai — balik dan kalikan.
Jika hasilnya pecahan tidak biasa seperti ²¹⁄₄, Anda boleh membiarkannya untuk aljabar atau tulisan formal, atau ubah jadi bilangan campuran (5 ¼) untuk kebutuhan sehari-hari.
Baik di kelas maupun dapur, menguasai cara menguraikan perhitungan ini membuat Anda siap menghadapi berbagai soal matematika, tak peduli seberapa rumit angkanya. Anda juga bisa memeriksa hasil langkah-langkahnya dengan Kalkulator Matematika.
Kapan Pecahan Menyelamatkan Proyek
Bilangan campuran tak hanya penting di ruang kelas — terkadang juga menyelamatkan waktu, biaya, dan proyek besar.
Seorang mandor konstruksi di Des Moines, Iowa, bercerita bagaimana satu kesalahan membaca ukuran hampir menggagalkan renovasi sekolah. Cetak biru menyebutkan 8 ⅜ inci untuk trim logam khusus. Seorang magang baru, yang belum paham konversi pecahan, membacanya sebagai 8,3 inci. Akibatnya? Sekelompok panel aluminium terlalu pendek — hampir ¹⁄₁₆ inci, cukup untuk gagal inspeksi.
Kesalahan itu membuat tim mengulang kerja selama seminggu penuh dan menghabiskan lebih dari $4,000 untuk bahan.
“Saya belajar dengan cara sulit — desimal tidak selalu teman Anda. Bilangan campuran adalah ukuran yang dipakai alat ukur sungguhan. Itu ⅜, bukan 0,375, dan perbedaan itu bisa merugikan gaji Anda.” — Tim Vega, pimpinan konstruksi, Vega & Sons Build Co.⁴
Sekarang, sebelum semua ukuran dikirim ke bengkel manufaktur, tim selalu memeriksa ulang dengan grafik konversi pecahan ke desimal yang ditempel di setiap kotak perkakas — dan pegawai baru mendapat pelajaran cepat tentang penjumlahan dan pengurangan bilangan campuran dengan penyebut umum.
Bilangan campuran bukan hanya teori. Mereka hadir dalam cetak biru, resep, faktur, statistik olahraga, dan kalibrasi alat. Memahami penggunaannya bukan soal lulus tes — tapi soal bergerak percaya diri dalam dunia nyata, dengan meteran di tangan.

- NASA. “Apollo 13 Timeline.”
U.S. Department of Education. “High School Math Study.”
Napa Valley College Baking & Culinary Program, wawancara anekdot, Maret 2023
Wawancara dengan Tim Vega, Juni 2022. Standar & Inspeksi Bangunan, Departemen Keamanan Publik Iowa

