Kalkulator Dasar Pecahan

Pecahan muncul di mana-mana—resep masakan, konstruksi, pajak, bahkan saat berbagi pizza. Menguasai perhitungan pecahan dapat menghemat waktu, mencegah kesalahan, dan meningkatkan kepercayaan diri baik bagi pelajar maupun profesional. Mulai dari menjumlahkan ⅔ + ¼ hingga mengalikan ⅝ × ¾, panduan ini menjelaskan setiap langkah, meluruskan kebingungan umum, dan menunjukkan bagaimana pecahan berkaitan dengan masalah dunia nyata.

Apa Itu Pecahan?

Pecahan adalah cara untuk menunjukkan bagian dari keseluruhan. Ditulis dengan dua angka bertumpuk, dipisahkan garis—angka atas disebut pembilang (bagian yang kita miliki) dan angka bawah penyebut (jumlah bagian yang membentuk keseluruhan).

Bayangkan pizza: jika dipotong menjadi 8 irisan sama besar dan Anda makan 3, berarti Anda telah memakan 3⁄8 pizza. Angka 3 menunjukkan jumlah irisan yang Anda makan, dan 8 menunjukkan total pizza.

Pecahan sering muncul di luar pelajaran matematika. Resep misalnya sering meminta ½ cangkir gula atau ¾ sendok teh garam. Pada konstruksi dan pengukuran pecahan dipakai terus—seperti papan setebal 5⁄8 inci. Bahkan saat membagi tagihan ke teman atau menghitung diskon, pecahan ikut berperan.

Contoh sehari-hari:

• Setengah pai: ½

• Tiga per empat tangki bensin: ¾

• Lima per delapan inci pada mistar: 5⁄8

Pecahan membuat angka lebih fleksibel—membantu menjelaskan hal yang tidak bisa dinyatakan dengan angka bulat.

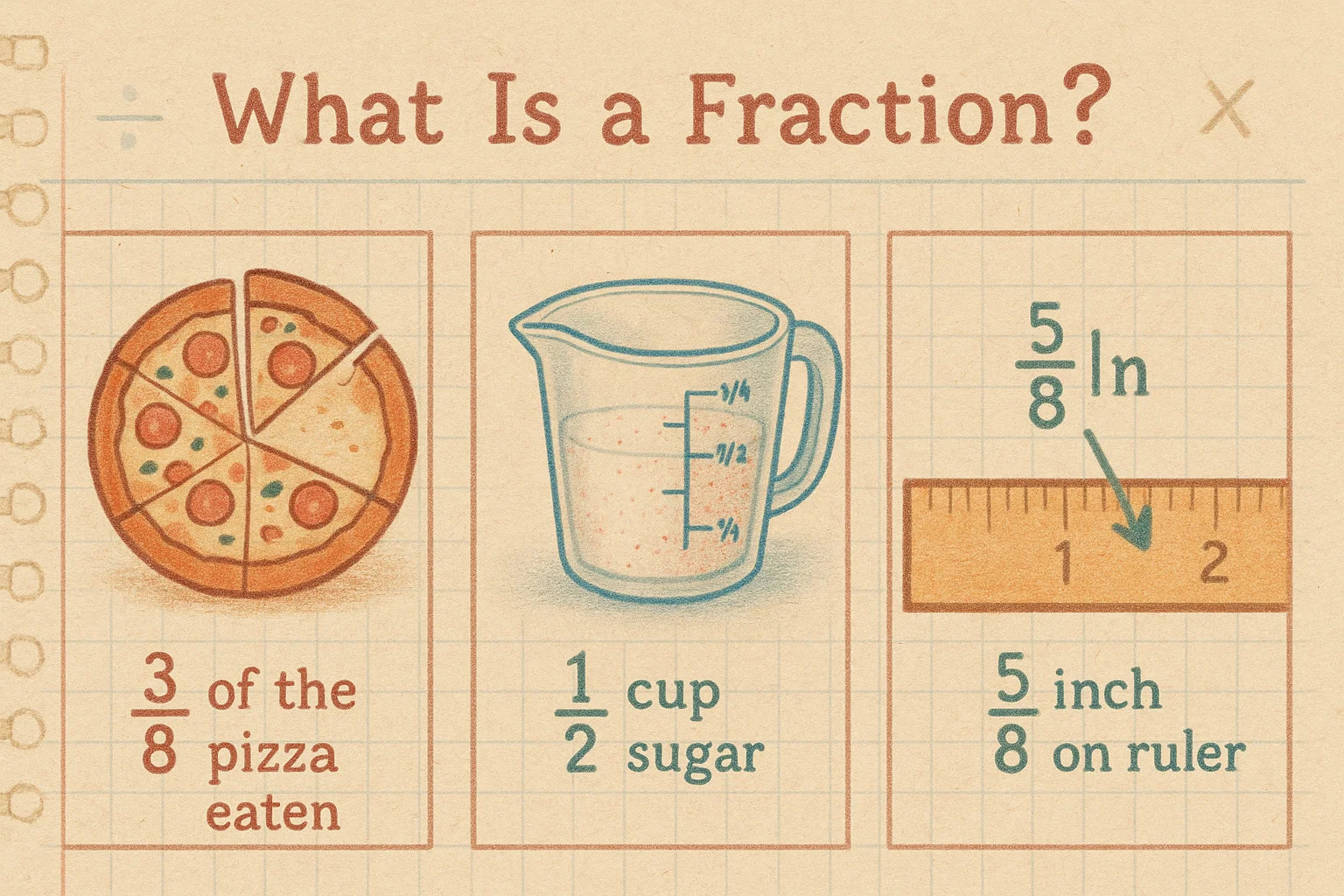
Menambahkan Pecahan

Menambah pecahan mudah jika kedua penyebut sama—cukup jumlahkan pembilang lalu biarkan penyebut tetap.

Contoh: 1⁄4 + 2⁄4 = 3⁄4

Saat penyebut berbeda, buat penyebutnya sama dulu. Cara termudah adalah cari penyebut bersama—biasanya kelipatan persekutuan terkecil (KPK). Lalu ubah pecahan supaya memiliki penyebut itu sebelum dijumlahkan.

Contoh penyebut berbeda: 1⁄3 + 1⁄6

• Penyebut bersama terkecil adalah 6.

• Ubah 1⁄3 menjadi 2⁄6.

• Sekarang jumlahkan: 2⁄6 + 1⁄6 = 3⁄6.

• Sederhanakan dengan membagi pembilang dan penyebut dengan 3: 3⁄6 = ½.

Trik cepat: jika satu penyebut merupakan kelipatan penyebut lain (misal 2 dan 4), langsung gunakan penyebut terbesar tanpa mencari KPK penuh.

Mengurangkan Pecahan

Pengurangan pecahan hampir sama dengan penjumlahan—hanya ganti tanda plus dengan minus.

Jika penyebut sama, kurangi pembilangnya lalu biarkan penyebut tetap:

5⁄8 − 3⁄8 = 2⁄8, yang disederhanakan menjadi 1⁄4.

Jika penyebut berbeda, cari penyebut bersama dulu (biasanya KPK), ubah tiap pecahan, lalu kurangi:

Contoh penyebut berbeda:
5⁄6 − 1⁄3

• Penyebut bersama adalah 6.

• Ubah 1⁄3 menjadi 2⁄6.

• Sekarang kurangi: 5⁄6 − 2⁄6 = 3⁄6.

• Sederhanakan: 3⁄6 = ½.

Jika pembilang pecahan kecil lebih besar setelah disamakan, hasilnya bisa negatif. Contoh:
1⁄4 − 3⁄4 = −2⁄4 = −½.

Catatan: Anda juga bisa menulis hasil negatif sebagai bilangan campuran jika perlu, tapi meninggalkannya sebagai pecahan tak wajar (−5⁄4) biasanya sudah diterima.

Mengalikan Pecahan

Perkalian pecahan sering jadi operasi termudah—tak perlu penyebut sama. Aturannya jelas: kalikan pembilang, kalikan penyebut, lalu sederhanakan hasilnya jika bisa.

Langkah demi langkah:

Contoh: 2⁄3 × 3⁄5

1. Kalikan pembilang: 2 × 3 = 6.

2. Kalikan penyebut: 3 × 5 = 15.

3. Gabungkan: 6⁄15.

4. Sederhanakan dengan membagi 3: 6⁄15 = 2⁄5.

Cara ini berlaku untuk pecahan benar (1⁄2) maupun tak wajar (7⁄4).

Contoh lain dengan angka lebih besar: 5⁄8 × 4⁄10

1. Pembilang: 5 × 4 = 20.

2. Penyebut: 8 × 10 = 80.

3. Gabungkan: 20⁄80.

4. Sederhanakan: bagi 20, hasilnya 1⁄4.

Trik berguna: batasi ukuran angka dengan mencoret silang sebelum dikalikan. Jika pembilang dan penyebut punya faktor bersama, sederhanakan dulu: 6⁄10 × 5⁄9

• Perhatikan 10 dan 5 punya faktor sama.

• Sederhanakan 5⁄10 jadi 1⁄2.

• Sekarang masalahnya 6⁄2 × 1⁄9 = 3 × 1⁄9 = 3⁄9 = 1⁄3.

Tahukah Anda?
Mengalikan dengan pecahan kurang dari 1 selalu menghasilkan angka yang lebih kecil. Misalnya, ¾ × ½ = ⅜, lebih kecil dari kedua pecahan awal.

Membagi Pecahan

Membagi pecahan mungkin terasa rumit, tapi sebenarnya hanya satu langkah ekstra dibanding mengalikan. Alih-alih membagi langsung, balik pecahan kedua (inversnya) lalu kalikan seperti biasa.

Aturan “balik lalu kalikan” ini selalu berhasil karena membagi dengan pecahan sama dengan mengalikan dengan inversnya.

Contoh: ¾ ÷ ½

1. Biarkan pecahan pertama: ¾.

2. Balik pecahan kedua (½ menjadi ²⁄₁).

3. Kalikan: ¾ × ²⁄₁ = ⁶⁄₄.

4. Sederhanakan: bagi pembilang dan penyebut dengan 2 jadi ³⁄₂.

5. Opsional: ubah ke bilangan campuran: 1½.

Contoh lain: ⁵⁄₆ ÷ ¹⁰⁄₉

1. Balik ¹⁰⁄₉ jadi ⁹⁄₁₀.

2. Kalikan: ⁵⁄₆ × ⁹⁄₁₀ = ⁴⁵⁄₆₀.

3. Sederhanakan: bagi 15, hasilnya ¾.

Cek cepat: membagi dengan pecahan kurang dari 1 biasanya membuat hasil lebih besar, sedangkan membagi pecahan lebih dari 1 membuatnya lebih kecil.

Hubungan dunia nyata: jika resep membutuhkan ¾ cangkir tapi Anda hanya ingin setengah resep, Anda sebenarnya melakukan ¾ ÷ 2. Menurut aturan itu, ¾ × ½ = 3⁄8 cangkir.

Fakta penting: Anda tidak perlu mencari penyebut bersama saat membagi pecahan. Selalu balik pecahan kedua dan kalikan—lebih cepat dan mengurangi kemungkinan salah.

Koneksi Operasi Pecahan dengan Konsep Matematika Lebih Besar

Pecahan mungkin terasa seperti mata pelajaran sekolah, tapi sebenarnya mereka muncul di mana pun Anda melihat—bukan hanya di ujian matematika. Saat Anda menambah, mengurang, mengali, atau membagi pecahan, Anda menggunakan ide yang terkait dengan kehidupan sehari-hari dan bahkan matematika tingkat lanjut tanpa menyadarinya.

Pikirkan:

• Perbandingan dan resep: Ketika Anda menyederhanakan ⁸⁄₁₂ menjadi ²⁄₃, Anda tidak hanya menyederhanakan—Anda menggambarkan rasio. Rasio itu bisa membantu menggandakan resep kue atau menyesuaikan bahan jika hanya ingin setengah adonan.

• Aljabar tanpa istilah menakutkan: Menyelesaikan x ÷ ¾ = 2 sebenarnya menggunakan trik yang sama—balik ¾ menjadi ⁴⁄₃ dan kalikan. Pecahan bekerja di balik layar untuk memecahkan persamaan.

• Konversi satuan yang sering dipakai: Pernah mengubah Fahrenheit ke Celsius? Rumusnya memakai ⁵⁄₉. Atau mengonversi mil per jam ke meter per detik—pecahan membuatnya mungkin.

• Peluang dan probabilitas: Melempar dadu enam sisi? Peluang muncul angka 4 adalah ¹⁄₆. Menghitung kemungkinan dua peristiwa seringkali melibatkan penjumlahan atau perkalian pecahan, walau kadang tak disadari.

Pecahan lebih dari sekadar angka bergaris—mereka alat untuk memahami hubungan, skala, dan perubahan. Setelah Anda menyadari seberapa sering pecahan muncul, mereka akan terasa bukan beban tugas, melainkan trik yang sudah Anda kuasai.

Fakta menarik: Orang Mesir kuno menulis hampir semua pecahan dengan pembilang 1. Untuk menulis ²⁄₃, mereka memecahnya jadi ½ + ¹⁄₆. Cara itu berhasil, tapi pecahan modern jauh lebih mudah dipahami.