Kalkulator Segitiga Siku-siku

Apa Itu Segitiga Siku-siku

Segitiga siku-siku adalah segitiga dengan satu sudut yang tepat 90°. Sudut siku-siku ini menghasilkan dua sisi, yang disebut kaki, yang bertemu di sudut tersebut, dan satu sisi yang lebih panjang di hadapannya, disebut hipotenusa. Dalam sebagian besar rumus, kaki biasanya diberi label a dan b, sementara hipotenusa dilabeli c.

Segitiga siku-siku sering ditemukan hampir di mana saja — dari kemiringan atap rumah hingga balok penyangga jembatan, atau bahkan bayangan yang dihasilkan oleh lampu jalan. Dalam matematika, segitiga ini sangat disukai karena memudahkan perhitungan sisi atau sudut yang hilang hanya dengan beberapa bilangan saja.

Yang membuatnya istimewa adalah hubungan alami antar ketiga sisinya. Berkat teorema Pythagoras, jika Anda mengetahui dua sisi, Anda selalu dapat menemukan sisi ketiga. Oleh karena itu, segitiga siku-siku menjadi dasar berbagai bidang mulai dari geometri dasar hingga trigonometri dan fisika.

Cara Menghitung Segitiga Siku-siku

Setiap segitiga siku-siku mengikuti satu aturan sederhana: a² + b² = c²

Ini adalah teorema Pythagoras, yang menghubungkan dua kaki (a dan b) dengan hipotenusa (c). Jika Anda mengetahui dua dari sisi ini, Anda selalu bisa menghitung yang ketiga.

Misalnya, jika kaki memiliki panjang 3 dan 4 satuan, hipotenusanya adalah:

c = √(3² + 4²) = √(9 + 16) = 5

Segitiga 3–4–5 ini adalah contoh klasik karena angkanya sederhana, namun aturan yang sama berlaku untuk semua segitiga siku-siku — bahkan yang memiliki bilangan desimal atau nilai besar.

Anda juga dapat mengubah rumus untuk mencari kaki yang hilang:

• a = √(c² − b²)

• b = √(c² − a²)

Versi singkat ini memudahkan perhitungan, baik saat bekerja manual maupun saat memeriksa ulang hasil.

Menentukan Sudut dalam Segitiga Siku-siku

Setelah sisi-sisi segitiga diketahui, menghitung sudut menjadi mudah dengan sedikit trigonometri. Cara cepat paling umum didapat dari rasio alami segitiga:

• Menggunakan tangen: θ = arctan(a⁄b) — cocok jika Anda tahu kedua kaki.

• Menggunakan sinus: θ = arcsin(a⁄c) — berguna jika diketahui satu kaki dan hipotenusa.

Fungsi-fungsi ini memudahkan menemukan sudut yang hilang. Setelah memiliki satu sudut lancip, sudut lainnya cukup 90° − θ.

Untuk pemeriksaan lebih lanjut atau eksplorasi, Anda dapat menggunakan alat terkait seperti Kalkulator Trigonometri agar proses perhitungan sudut lebih cepat.

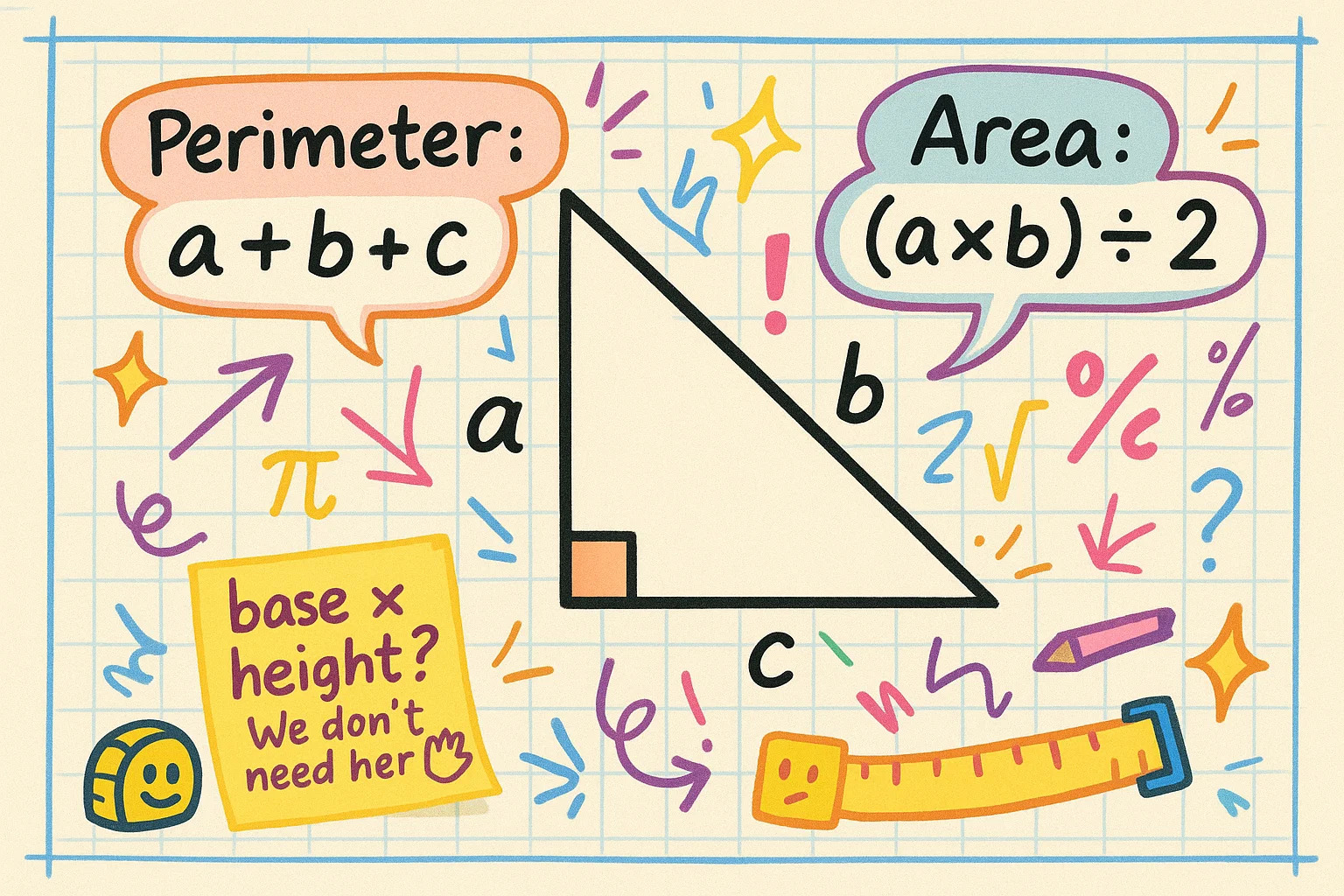
Keliling dan Luas Segitiga Siku-siku

Setelah mengetahui sisi-sisi segitiga siku-siku, menghitung keliling dan luasnya sangat mudah. Keliling merupakan jumlah ketiga sisi: P = a + b + c

Untuk luas, ada cara singkat yang berlaku untuk semua segitiga siku-siku: A = (a × b) ÷ 2

Karena kedua kaki membentuk sudut siku-siku sempurna, keduanya berperan sebagai alas dan tinggi, sehingga Anda tidak memerlukan rumus tambahan atau garis tinggi.

Misalnya, jika segitiga memiliki kaki dengan panjang 6 dan 8 satuan, maka hipotenusa c adalah 10 (berdasarkan teorema Pythagoras). Kelilingnya adalah 6 + 8 + 10 = 24, dan luasnya (6 × 8) ÷ 2 = 24.

Rumus-rumus ini memudahkan pengukuran cepat segitiga, baik saat mengerjakan tugas, menyusun rencana konstruksi, atau bahkan merancang proyek DIY.

Rasio Segitiga Siku-siku yang Umum

Beberapa segitiga siku-siku muncul sangat sering dalam matematika maupun kehidupan sehari-hari sehingga layak untuk dihafal. Segitiga “khusus” ini memiliki rasio sisi yang tetap, artinya Anda dapat melewatkan perhitungan tambahan dan menemukan sisi atau sudut yang hilang hampir seketika.

Dua yang paling umum adalah:

1. Segitiga 30°–60°–90°

• Rasio sisi selalu mengikuti pola 1 : √3 : 2.

• Sisi terpendek (berhadapan dengan 30°) adalah ukuran referensi — kalikan dua untuk mendapatkan hipotenusa, dan kalikan dengan √3 untuk kaki yang lebih panjang.

• Kedua kaki sama panjang, dan hipotenusa selalu kaki × √2.

• Rasionya adalah 1 : 1 : √2.

Tabel referensi cepat:

Mengenali pola ini dapat menghemat waktu, terutama saat mengerjakan masalah geometri atau trigonometri.

Ingin mempraktikkan lebih banyak soal segitiga? Coba Kalkulator Matematika, Kalkulator Teorema Pythagoras, dan Kalkulator Trigonometri.