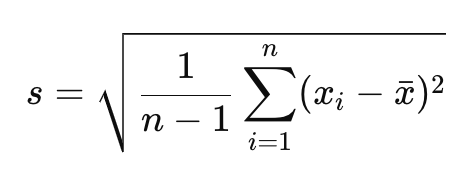Kalkulator Deviasi Standar

Deviasi standar mungkin salah satu istilah yang pernah Anda dengar di sekolah — entah saat pelajaran matematika atau tertulis di laporan penelitian. Namun di balik nama yang terkesan rumit ini terdapat konsep yang sebenarnya sangat intuitif dan berperan penting dalam segala hal, mulai dari penemuan ilmiah hingga strategi bisnis dan prakiraan cuaca. Secara sederhana, deviasi standar membantu kita memahami sebaran — seberapa jauh nilai-nilai menyimpang dari pusat, entah itu nilai ujian, harga, atau hasil pasien. Mengetahui cara mengukur variabilitas memberi kita kejelasan, konteks, dan keyakinan pada data yang kita gunakan sehari-hari.

Lihat Matematika untuk menemukan lebih banyak kalkulator

Apa Itu Deviasi Standar?

Deviasi standar mengukur seberapa tersebar nilai-nilai dalam satu himpunan data. Anggap saja ini cara untuk menjawab pertanyaan: “Seberapa jauh angka-angka menyimpang dari rata-rata?”

Bayangkan seorang guru memberi kuis dan seluruh kelas meraih skor tepat 80 dari 100. Rata-ratanya 80, dan setiap murid mendapatkan angka itu — jadi deviasi standarnya nol. Tidak ada variabilitas sama sekali. Sekarang bayangkan kelas kedua dengan rata-rata yang sama, 80, tapi nilai nyatanya 60, 70, 90, dan 100. Meskipun rata-ratanya masih 80, nilainya sangat bervariasi. Kelas kedua itu punya deviasi standar yang jauh lebih tinggi.

Deviasi standar rendah berarti titik data berkumpul rapat di sekitar rata-rata; deviasi standar tinggi berarti sebarannya lebih luas.

Mengapa Variabilitas Data Penting?

Variabilitas bukan sekadar ‘noise’ statistik — ia menceritakan kondisi sebenarnya. Dengan mengukur fluktuasi data, deviasi standar membantu kita melihat tren, deteksi nilai ekstrim, dan pola tersembunyi. Di bidang kesehatan, ini dipakai untuk menilai konsistensi efek suatu pengobatan. Dalam sains iklim, deviasi standar melacak perubahan suhu yang tidak biasa seiring waktu. Para pendidik menggunakannya untuk menganalisis prestasi murid antar sekolah, sementara insinyur menerapkannya dalam kontrol kualitas. Tanpa memahami variabilitas, kita berisiko salah tafsir apa yang sesungguhnya dikatakan data.

Coba alat terkait: Kalkulator Rata-rata, Kalkulator Varians, atau Kalkulator Z-Score untuk mengeksplorasi lebih banyak cara data bercerita.

Deviasi Standar Populasi

Saat Anda memiliki data dari seluruh populasi yang dipelajari, Anda bisa menghitung deviasi standar populasi tanpa perlu mengestimasi. Metode ini memberi derajat variabilitas yang tepat untuk keseluruhan data, misalnya ketika Anda memiliki data dari semua individu dalam populasi atau semua titik dalam survei menyeluruh.

Rumus deviasi standar populasi:

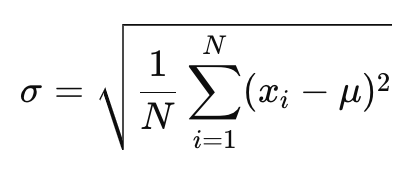
Di mana:

𝜎: deviasi standar populasi,

𝑁: jumlah pengamatan dalam dataset (ukuran populasi),

x_i: setiap nilai dalam dataset,

𝜇: rata-rata populasi.

Deviasi Standar Sampel

Ini digunakan ketika Anda hanya memiliki sampel data yang mewakili populasi. Karena tidak mungkin mendapatkan data seluruh populasi, deviasi standar sampel membantu memperkirakan deviasi standar populasi berdasarkan data sampel yang ada. Deviasi standar sampel menyertakan koreksi untuk memperhitungkan kemungkinan bias dalam estimasi, agar ukuran sebaran tidak diremehkan.

Rumus deviasi standar sampel:

Di mana:

𝑠: deviasi standar sampel,

𝑛: jumlah pengamatan dalam sampel,

x̄: rata-rata sampel.

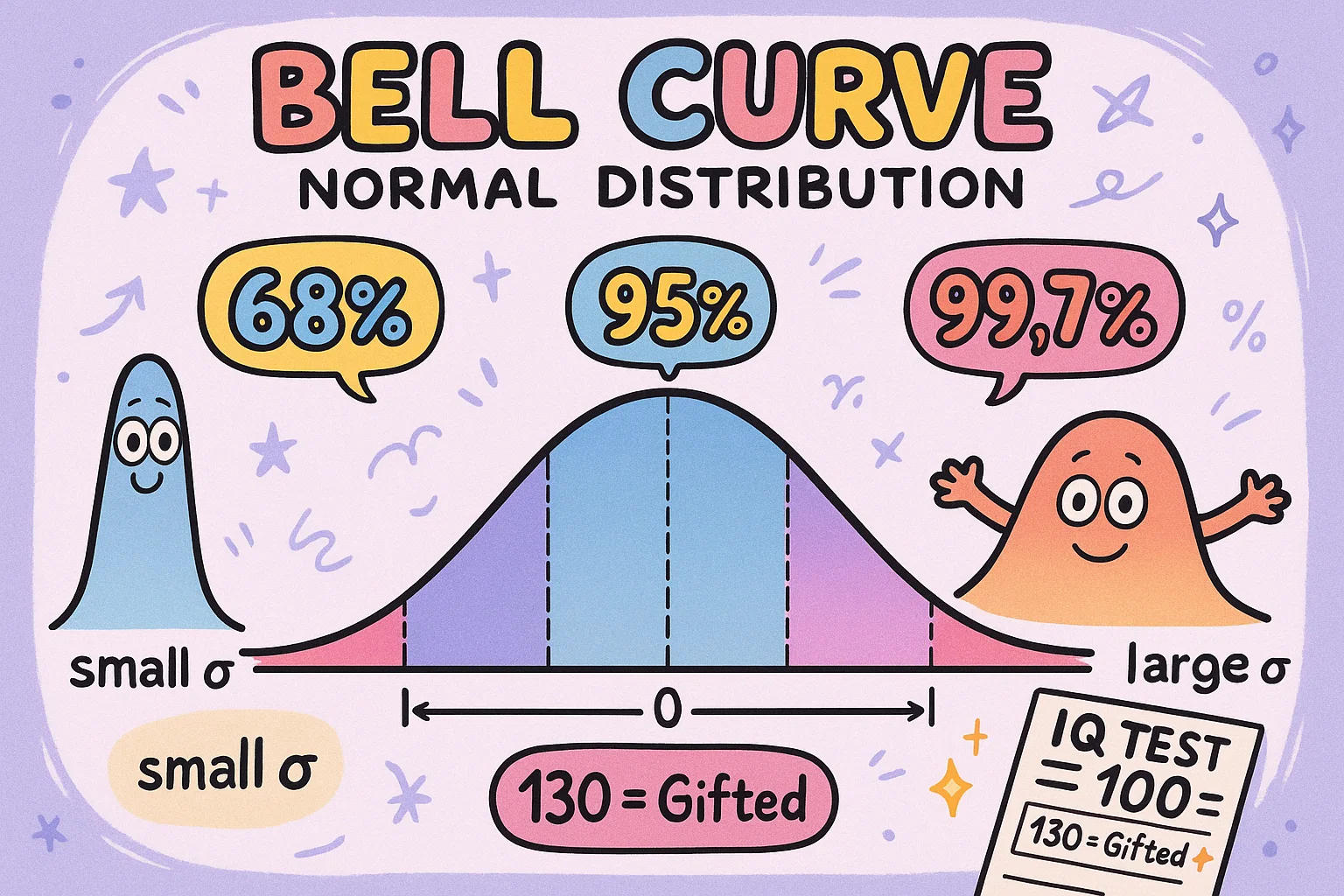
Kurva Lonceng dan Distribusi Normal

Anda mungkin pernah melihat kurva lonceng — grafik berbentuk bukit halus di mana sebagian besar nilai berada di tengah dan semakin sedikit di ujung-ujungnya. Kurva ini lebih dari sekadar bentuk indah. Ia menggambarkan distribusi normal, yang sering muncul di kehidupan nyata: tinggi badan, skor IQ, hasil ujian, bahkan tekanan darah.

Di sinilah peran deviasi standar. Ia mengatur seberapa lebar atau sempit bentuk lonceng itu. Jika kebanyakan angka dekat rata-rata, kurvanya akan sempit dan tinggi — menandakan deviasi standar kecil. Namun jika angka-angka lebih tersebar, kurva melebar dan memendek, artinya deviasi standar besar.

Ada aturan praktis untuk ini:

• 68% nilai berada dalam 1 deviasi standar dari rata-rata

• 95% dalam 2 deviasi standar

• Dan 99,7% dalam 3 deviasi standar

Ini membuatnya sangat mudah memahami seberapa umum (atau tidak biasa) sebuah angka — baik saat menganalisis nilai ujian maupun imbal hasil saham.

🎯 Fun Fact: Kebanyakan tes IQ dirancang agar skornya mengikuti kurva lonceng — dengan rata-rata 100 dan deviasi standar 15. Itulah sebabnya skor 130 dianggap jenius!